문제 : https://www.acmicpc.net/problem/2458
이 문제는 자신의 키가 몇번째인지 정확하게 순위를 구할 수 있는 학생 수를 구하는 문제다.
플로이드-워셜
import sys
input = sys.stdin.readline
N, M = map(int, input().split()) # 학생의 수 N, 키 비교 횟수 M
matrix_big = [[0 for _ in range(N+1)] for i in range(N+1)] # 키 큰 사람 구하기
matrix_small = [[0 for _ in range(N+1)] for i in range(N+1)] # 키 작은 사람 구하기
# 인접 행렬 저장
for i in range(M):
a, b = map(int, input().split())
matrix_big[a][b] = 1 # 키가 작은 학생 -> 큰 학생
matrix_small[b][a] = 1 # 키가 큰 학생 -> 작은 학생
# 플로이드-워셜 알고리즘
for k in range(1, N+1):
for i in range(1, N+1):
for j in range(1, N+1):
if(i==j): # 같은 학생일 때 지나가기
continue
# 키 큰 사람 업데이트
if(matrix_big[i][k]+matrix_big[k][j] > 1): # 경로가 존재 시
matrix_big[i][j] = 1
# 키 작은 사람 업데이트
if(matrix_small[i][k]+matrix_small[k][j] > 1): # 경로가 존재 시
matrix_small[i][j] = 1
# 순위를 알 수 있는 사람 구하기
count = 0
for i in range(1, N+1):
if(sum(matrix_big[i])+sum(matrix_small[i]) > N-2): # 모든 사람들과 관계가 있으면
count += 1
print(count)
[문제풀이]
이를 구하기 위해선 모든 (A, B)에 대해 A에서 B로 갈 수 있는 경로를 알 수 있는 플로이드-워셜 알고리즘을 사용한다.
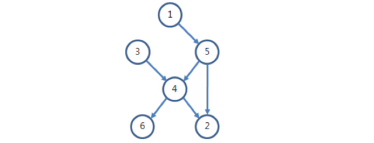
위는 키의 비교 결과를 가지고 그린 그래프이다.
키가 작은 학생에서 큰 학생으로 화살표를 그려서 표현하였다.
즉, 경로가 연결되어 있으면 자신보다 키가 큰 사람이란 뜻이다.
그러나 이 그래프는 단방향 그래프이기 때문에 키가 큰 학생만 구할 수 있다.
그렇다고 양방향으로 그래프를 그릴 경우 모든 사람들의 경로가 연결되어 버린다.
그래서
Graph 1. 키가 작은 학생-> 큰 학생
Graph 2. 키가 큰 학생-> 작은 학생
이렇게 그래프를 각각 나눠서, 자신보다 키가 큰 사람, 작은 사람을 각각 구함!
# 키 큰 사람 업데이트
if(matrix_big[i][k]+matrix_big[k][j] > 1): # 경로가 존재 시
matrix_big[i][j] = 1
# 키 작은 사람 업데이트
if(matrix_small[i][k]+matrix_small[k][j] > 1): # 경로가 존재 시
matrix_small[i][j] = 1
그 후, 자신보다 키가 큰 사람 수 + 작은 사람 수 >= 전체 사람수 -1 인 경우 순위를 구할 수 있는 사람이므로 사람 수를 구해준다.
if(sum(matrix_big[i])+sum(matrix_small[i]) > N-2): # 모든 사람들과 관계가 있으면
count += 1이는 python으로 할 경우 플로이드-워셜 알고리즘의 시간 복잡도로 인해 시간 초과가 뜬다....
PyPy3으로 할 것!
BFS (너비 우선 탐색)
import sys
from collections import deque
input = sys.stdin.readline
N, M = map(int, input().split()) # 학생의 수 N, 키 비교 횟수 M
B_Tree = [[] for i in range(N+1)] # 인접 리스트
S_Tree = [[] for i in range(N+1)] # 인접 리스트
# 인접 리스트 저장
for i in range(M):
a, b = map(int, input().split())
B_Tree[a].append(b)
S_Tree[b].append(a)
# BFS 구현
def BFS(start, tree, visited):
q = deque([start])
while q:
v = q.popleft()
for i in tree[v]:
if not visited[i]:
visited[i] = True
q.append(i)
# 순위 알 수 있는 사람 탐색
def init():
B_visited = [False]*(N+1)
S_visited = [False]*(N+1)
return B_visited, S_visited
count = 0
for i in range(1, N+1):
B_visited, S_visited = init() # 배열 초기화
# 탐색 알고리즘 수행
BFS(i, B_Tree, B_visited) # 키가 큰 학생 탐색
BFS(i, S_Tree, S_visited) # 키가 작은 학생 탐색
if(sum(B_visited)+sum(S_visited) > N-2): # 모든 학생들의 순서를 알 수 있으면
count += 1
print(count)
[문제풀이]
BFS, DFS 같은 탐색 알고리즘을 사용해서 풀 수도 있다.
이 방식도 플로이드-워셜 알고리즘을 쓸 경우와 원리가 같다.
1. 큰 학생-> 작은 학생, 작은 학생-> 큰 학생으로 연결되는 인접 리스트를 각각 만든다.
2. BFS 알고리즘을 사용해 출발한 노드에서부터 갈 수 있는 노드들을 표기하는 visited 배열을 만든다.
3. 각 노드들을 BFS 알고리즘을 사용해 구한다.
4. 순서를 알 수 있는 학생을 count!
키가 작은 학생, 큰 학생을 각각 탐색해 키가 큰 사람 수 + 작은 사람 수 >= 전체 사람수 -1인 경우 순서를 알 수 있는 사람이므로 사람 수를 구해준다.
사용한 알고리즘이 탐색 알고리즘일 뿐 원리는 동일하며, DFS를 사용해도 무방하다.
시간 복잡도가 O(N^3)인 플로이드 워셜에 비해 훨씬 빠르며, python으로도 시간 초과 안나고 돌릴 수 있음!
'코딩테스트 > 백준' 카테고리의 다른 글
| [백준] 11403번 : 경로 찾기 (Python) (1) | 2024.12.26 |
|---|---|
| [백준] 11404번 : 플로이드 (Python) (0) | 2024.12.26 |
| [백준] 1956번 : 운동 (Python) (0) | 2024.12.26 |
| [백준] 2839번 : 설탕 배달 (Python) (0) | 2024.12.26 |
| [백준] 1978번 : 소수 찾기 (Python) (0) | 2024.12.26 |